

Aposto que você já falou/ouviu a seguinte expressão: “Que mundo pequeno!”. Mas quantas pessoas eu teria que conhecer para ser apresentada a uma pessoa ilustre como Betinha, Rainha da Inglaterra? Em 1967 o sociólogo Stanley Milgram teve um “eureca” com esse dito popular do mundo pequeno e resolveu testar uma hipótese. Ele acreditava que todas as pessoas estão a todo momento alguns graus de separação de qualquer outro indivíduo no mundo. Mesmo que eu não te conheça, devo conhecer alguém que conhece alguém que conhece você. A principal pergunta de Milgram era: quantos “alguéns” há no caminho?
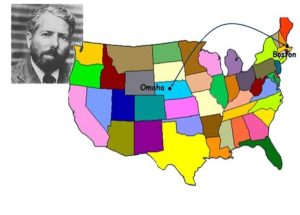 Para responder essa questão, ele enviou para pessoas aleatórias em Omaha (Nebraska), 160 cartas solicitando que eles enviassem esta mesma carta para um destinatário específico e desconhecido: um corretor em Boston. Se a pessoa não conhecesse o destinatário, ela deveria enviar a carta para alguém que achasse que estaria mais perto do destino. Ele observou que, das cartas que chegaram, a maioria passou por poucas pessoas até chegar no destinatário final; concluindo que os graus de separação entre as pessoas eram em média seis graus. E não é que era pequeno mesmo? E assim nasceu a teoria modelo “Small World” (mundo pequeno).
Para responder essa questão, ele enviou para pessoas aleatórias em Omaha (Nebraska), 160 cartas solicitando que eles enviassem esta mesma carta para um destinatário específico e desconhecido: um corretor em Boston. Se a pessoa não conhecesse o destinatário, ela deveria enviar a carta para alguém que achasse que estaria mais perto do destino. Ele observou que, das cartas que chegaram, a maioria passou por poucas pessoas até chegar no destinatário final; concluindo que os graus de separação entre as pessoas eram em média seis graus. E não é que era pequeno mesmo? E assim nasceu a teoria modelo “Small World” (mundo pequeno).
Para entender cientificamente essa relação, usaremos a teoria de grafos (Leonhard Euler – 1736). A teoria de grafos envolve um modelo matemático para representar relações entre pares de objetos. Um grafo é um diagrama (representação visual) de uma rede. Uma rede é um conjunto de objetos que se relacionam entre si. Seus principais elementos são os nós (os pontinhos que representam os objetos) e as arestas (linhas que representam as interações entre os objetos).
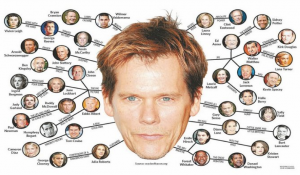 De acordo com o IMDB (Internet Movie Database), entre 1898 e 2000, cerca de 500 mil pessoas atuaram em filmes, totalizando algo como 200 mil produções. Foi feita uma rede com esses 500 mil atores que podem ser conectados ao ator Kevin Bacon por poucos filmes. Atores são os nós da rede, e há uma aresta ligando dois atores, se eles participaram em ao menos um filme junto. Se você atuou num filme com Kevin Bacon, seu número Bacon é 1. Se atuou com alguém que atuou com ele, seu número Bacon é 2, e assim por diante. O objetivo do jogo é determinar o menor número Bacon possível de um certo ator até o Kevin. A descoberta? Em um mundo com milhares de indivíduos, todo ator poderia ser conectado a qualquer outro ator numa média de menos de quatro passos.
De acordo com o IMDB (Internet Movie Database), entre 1898 e 2000, cerca de 500 mil pessoas atuaram em filmes, totalizando algo como 200 mil produções. Foi feita uma rede com esses 500 mil atores que podem ser conectados ao ator Kevin Bacon por poucos filmes. Atores são os nós da rede, e há uma aresta ligando dois atores, se eles participaram em ao menos um filme junto. Se você atuou num filme com Kevin Bacon, seu número Bacon é 1. Se atuou com alguém que atuou com ele, seu número Bacon é 2, e assim por diante. O objetivo do jogo é determinar o menor número Bacon possível de um certo ator até o Kevin. A descoberta? Em um mundo com milhares de indivíduos, todo ator poderia ser conectado a qualquer outro ator numa média de menos de quatro passos.
Na biologia da conservação, a teoria de grafos é aplicada, por exemplo, nas redes de interações ecológicas. Numa rede alimentar, as espécies estão, em média, a dois graus de separação umas das outras. É possível utilizar estas redes em modelos de conservação de biodiversidade e conservação genética em paisagens fragmentadas. Assim, é possível prever respostas de comunidades ecológicas perante diferentes tipos de alterações ambientais (locais e/ou globais) e mudanças na composição da própria rede (como a extinção de uma espécie). Fazemos parte de uma grande rede de interações ecológicas que envolve milhares de espécies. A conservação dos elos dessa grande rede é essencial para o funcionamento dela e para a manutenção dos seus benefícios. As redes podem estabelecer o padrão fundamental para entender a biodiversidade e o impacto das políticas ambientais de conservação das espécies.
A biodiversidade endêmica (só existe lá) do arquipélago de Galápagos, por exemplo, é ameaçada pela introdução de espécies exóticas. Através das redes de interações, os pesquisadores conseguiram identificar que 20% de todas espécies agrupadas na rede (60 plantas e 220 polinizadores) eram exóticas, estando envolvidas em 38% das interações. A maioria das espécies eram insetos, especialmente dípteros (36%), himenópteros (30%) e lepidópteros (14%). Esses insetos exóticos tinham mais ligações do que polinizadores nativos (endêmicos ou não). Espécies exóticas podem deslocar a biodiversidade da ilha, atrapalhar interações ecológicas nativas, e afetar profundamente a estrutura e dinâmica da comunidade.
Com o avanço das redes complexas, é possível analisar desde os tamanhos necessários das reservas até o impacto humano em habitats naturais, e oferecer rotas alternativas de respostas às perturbações. O verdadeiro desafio de conservar a biodiversidade e suas funcionalidades não é apenas focar nas espécies em si, mas na manutenção e restauração das interações entre as redes. Entretanto, vários desafios práticos precisam ser superados antes que o objetivo de conservar as redes de interação entre espécies possa ser alcançado.
Texto por Msc. Tainah Cruz Moreira — publicado em junho de 2020.
Imagem destaque: Connected World por Sourajit Sengupta
Imagem 1: As complexas redes – José Garcia Vivas Miranda
Imagem 2: Six degrees of Kevin Bacon CLI Application
Imagem 3: Traveset et al. 2013
Disponível em: < https://universoracionalista.org/small-world-e-ws/>. Acessado em 06 de junho de 2020
Disponível em: < http://www.thegamewiz.com/strategy-games/kevin-bacon-six-degrees-connections/>. Acessado em 06 de junho de 2020
Disponível em: < : https://blog.dp6.com.br/introdu%C3%A7%C3%A3o-a-redes-complexas-df73b623d67f>. Acessado em 06 de junho de 2020
Hotta, L. A. (2017). Modelos ecológicos em redes complexas. Dissertação de Mestrado, Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, São Carlos. Recuperado em 2018-05-24, de http://www.teses.usp.br/teses/disponiveis/55/55134/tde-17112017-105116/
Traveset, A., Olesen, J. M., Nogales, M., Vargas, P., Jaramillo, P., Antolín, E., … & Heleno, R. (2015). Bird–flower visitation networks in the Galápagos unveil a widespread interaction release. Nature communications, 6, 6376.
Battist, C. Frammentazione ambientale, connettivita’, reti ecologiche: un contributo teorico e metodologico con particolare riferimento alla fauna selvatica. Provincia di Roma: Assessorato alle politiche ambientali, Agricoltura e Protezione civile, 2004. 249 p.
Universidade Estadual do Sudoeste da Bahia
Rua José Moreira Sobrinho, s/n
Bairro Jequiezinho – CEP 45.208 – 091
Campus Jequié

